Overview

These are notes that I am making while learning the finite-volume method (FVM). The methods discussed are based on the the book by W. Hundsdorfer and J. G. Verwer, Numerical solutions of time-dependent advection-diffusion reaction equations.

See the the accompanying project on Github for implementation of the solvers in Python branch, http://danieljfarrell.github.come/FVM/.

Finite volumes vs. finite differences

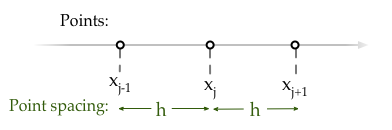
When first starting to solve (partial) differential equation problems a student will first encounter the finite difference method (FDM). The FDM relies on approximating the a differential operator as a series of distinct points,

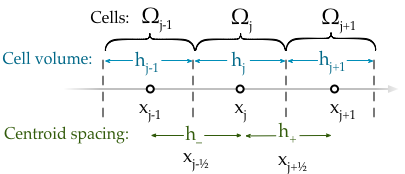
In contrast, the FVM uses a fundamental unit of averages over small spatial elements, or cells,

Although this distinction may seem trivial at first or even over complicated it is a particularly power technique when applied to conservation equations because the conservative properties of the governing equation are maintained even at the discretised level without introducing any approximations. This property is achieved by symbolic integrating the equations over a finite volume, then using solve the problem in terms of the integrated variables.

This sounds much more complicated that it is, let’s look at an example.